Lojistikte Gezgin Satıcı Problemi – İmkansızı hesaplayın
Bilgi Teknolojilerinin (BT) gelişmesi sayesinde şirketlerin giderek daha iyi satış sonuçları elde ettiği ve yazılım çözümleri sayesinde her şeyi çok daha rahat yapabildikleri iyi bilinmektedir. Dahası, insanlar giderek daha fazla meseleyi halledebiliyor veya internet üzerinden çalışabiliyor. Ancak, herkes bilgisayar biliminin bile sınırları olduğunu ve chatGPT dahil her şeye kesin bir cevap veremeyeceğini bilmiyor :).
Bilgisayar bilimleri alanında, yıllardır henüz verimli ve temel çözümler önerilmemiş konular ve sorunlar var. Bunlardan biri de TSL (Transport Spedition Logistics) endüstrisi ile yakından ilişkili olan gezgin satıcı problemi olarak adlandırılan optimizasyon problemidir. Bu konuda daha fazla bilgi edinmek için okumaya devam edin. Belki de bu problemi çözen şanslı kişi siz olacaksınız.
“Gezgin Satıcı Problemi” nasıl ortaya çıktı?
Gezgin satıcı problemini (TSP) çözmek için bir dizi talimat belirtmenin zorluğunu ilk duyuran kişiyi belirlemek zordur. Problemden ilk bahsedilen tarih 1830’lara kadar uzanmaktadır ve problemi çözmeye yönelik ilk girişimler yaklaşık 100 yıl sonra bir okul otobüsü için en uygun rotayı bulmaya çalışırken yapılmıştır. Karmaşık matematiksel yasalara ve ifadelere dayanan problemin analizini bilim insanlarına bırakacağız. Bu yüzden problemi kolay anlaşılır bir şekilde sunarak özüne odaklanacağım.
TSP problemi nedir?
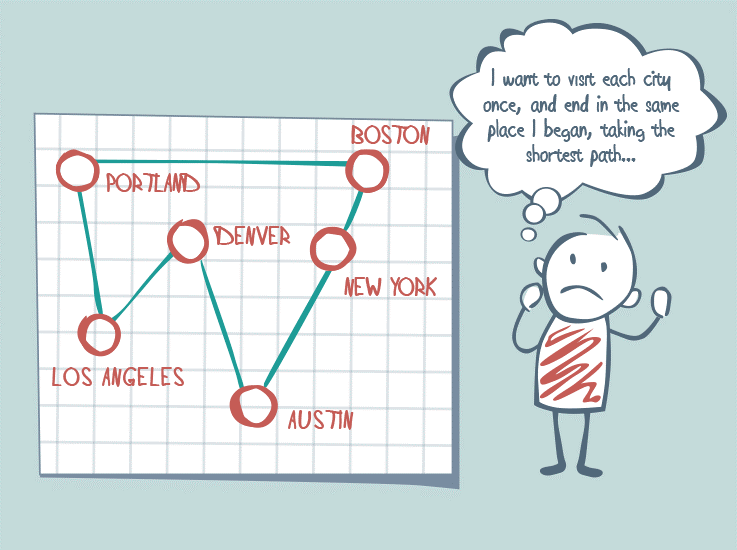
Boston’da işe başlayıp biten bir kurye olduğunu varsayalım. Bir gün New York, Denver, Los Angeles, Austin, Portland ve Chicago’daki adreslere paket teslim etmesi gerekiyor. Gezgin satıcı problemi, kuryenin tüm bu şehirleri ziyaret etmesini sağlayan en kısa rotayı bulmaktan ibarettir. Sadece rotanın uzunluğuyla ilgili olmak zorunda değildir, en ucuz veya en hızlı yolu bulmaya da odaklanabilir. Örneğimizde olası rota sayısı 5040’tır.
Şirketler TSP sorunuyla nasıl başa çıkıyor?
Birkaç şehir için en kısa rotayı arıyorsak, en uygun çözümü bulmak sıradan bir bilgisayarda saniyeler veya birkaç dakika sürebilir. Ancak, örneğin 52 şehirden bahsediyorsak, lojistik için yeterli olan yaklaşık çözümleri bulmak için çeşitli algoritmalar, paralel ve dağıtık hesaplama kullanılır, çünkü olası tüm rotaları kontrol etmek pratikte imkansızdır. Yapay zekanın (AI) bu konuda bir rol oynamasına muhtemelen şaşırmayacaksınız.
Gezgin Satıcı Probleminin Uygulamaları
Gezgin satıcı probleminin birçok pratik uygulaması vardır. Bunlardan en önemlisi ve bu makalenin yazılma nedeni, araç, gemi veya uçak filoları için rotaların optimizasyonu, maliyetlerin ve teslimat süresinin en aza indirilmesidir. Bir diğer uygulama ise depolardaki veya lojistik merkezlerindeki robotlar için rota planlamasıdır. TSP, optimum sinyal kalitesini sağlamak ve maliyetleri en aza indirmek için telekomünikasyon ağlarının tasarımında da kullanılır.
Yüklemenizi optimize etmenize yardımcı olacağız
Gezgin satıcı problemini çözemeyebilir ve herhangi bir sayıda şehir için en uygun rotayı bulamayabiliriz, ancak EasyCargo adında kargo yükleme planlaması için bir programımız var. Malların düzenlenmesi (boşaltma yerlerine göre gruplayabilirsiniz) ve yük dağılımı için en uygun planı oluşturmanın yanı sıra, Excel veya PDF formatında raporlar oluşturmanıza olanak tanır. Kargo yükleri üzerinde meslektaşlarınızla işbirliği çalışması için genel bir bağlantı bile mevcuttur.
Ayrıca, API’mizi kullanarak EasyCargo’yu şirket yazılımınızla veya FleetUp telemetri sistemi gibi diğer programlarla entegre edebilirsiniz. Bu bağlantıdan detayları hakkında daha fazla bilgi edinebilirsiniz.

Kaynak: https://developer-blogs.nvidia.com/wp-content/uploads/2023/01/cuopt-featured.jpg
One could actually say that for the TSL industry, the traveling salesman problem is slowly becoming less of a worry thanks to the development of artificial intelligence and Big Data. All kinds of delivery route optimization software offer a route that does not deviate significantly from the most favorable one and dynamically adjusts it in real time depending on the conditions on the roads.
Good luck with proposing an algorithm that can find the optimal route for any number of cities in polynomial time!




